Speed of Light in Relativity.

The Integrity of Theory.^[1][2]

Our wishful thinking credits scientific theories with being universally and eternally true; in fact, they are no more than our present best guess based on known evidence. If new empirical evidence is contrary to old theory, then the old theory must give way to revision or replacement. To say that evidence failing to refute a theory is a confirmation of the theory is misleading; other evidence could yet come to light and reveal a flaw in the theory. A correction following a successful refutation of a theory is to be celebrated as an advance toward truth.

For over a century, Einstein's relativity has been extraordinarily acclaimed, notwithstanding that for most practical matters classical relativity suffices and is still used. Real tests and actual applications of Einstein's relativity are rare. There are confirmations of some aspects of the theory, not of all aspects. The claimed isotropy of one-way light speed, independent of frame of reference, has never been confirmed. The oft made remark that relativity has been consistently confirmed is a denial of light speed anisotropy evident in the Sagnac effect and stellar spectroscopy. A further test, capable of measuring anisotropy, is the subject of this essay.

About the Author.

As a student in training to teach secondary school science, I hoped to understand Einstein's relativity. The explication of it in my modern physics textbook was inconsistent, convincing me that the author was faking understanding. When I appealed to the professor, he declined to discuss the topic but invited me to seek satisfaction from among six other texts that he lent me; all offered similarly inconsistent treatments of the subject. I was convinced that the only way I would achieve my goal was to read original sources. Three years later I read Einstein's special relativity paper of 1905. I was astounded to find his logic even more egregiously muddled than the textbooks. Recognising mathematical error and logical error, both well represented in his paper, do not require arcane or esoteric knowledge. So many others swore by the theory, I hoped they had corrected the muddle, and I sought their counsel. I encountered impatience and fallaceous argument in lieu of clarification. It was as if everyone either avoided the subject or feigned understanding. Popularized accounts of relativity theory were inconsistent one with another. So I began my independent quest for tests of the more dubious claims of the theory.

Through the years, I have erred, occassionally offering flawed arguments for rejecting the theory, and I have had the errors pointed out by the rare few physicists generous enough to consider my work. With gratitude, as well as with some inevitable embarrassment, I accept correction. On the other hand, being told my ideas must be wrong by persons ignorant of my ideas is simply vexing. The test concept presented herein has matured over several years and seems unassailable. It is, however, only a proposed test, which I, being retired and now of advanced age, shall never carry out myself.

Determination of absolute velocity, meaning velocity relative to the unique frame of reference for which one-way light speed is isotropic, can now be undertaken using atomic clocks to time one-way light travel. When the subtleties of this undertaking are properly understood, success will follow.

Throughout this essay, “speed of light” means speed in vacuo, not in refractive media.

What is a Relativity Theory?

All theories of relativity prescribe a method for transforming the time-and-place of an event specified relative to one frame of reference into the time-and-place specification of the same event relative to another frame of reference. Two persons walking in the aisle of a railway car may be moving at one meter per second in opposite directions relative to the car but in the same direction at eighteen and twenty meters per second, respectively, relative to the track.

Essential to any relativity theory is a set of definitions or standards for measure of time and distance and assumptions about the physical entities invoked therein. When Albert Einstein published his special relativity theory in 1905, the standard unit of time was the mean solar day, and the standard unit of distance was the one meter length of a particular platinum-iridium bar. The definitions have changed. Now time is based on cesium atomic clocks,^[3] and distance is defined in terms of light wavelengths.^[4]

Standard length determinations are now done interferometrically, involving a round trip of light rather than a one-way trip. Radar ranges are round-trip, consistent with standard distance determinations. A non-standard method that employs pseudoranges, one-way timings of light signals rather than standard distance determinations, is used to compute orbits of GPS satellites.

Our intuitive notion of relativity does not recognize a time difference between reference frames, but modern relativity theory does, needlessly. Designating a particular frame of reference as the standard for synchronizations and time determintions to be shared by all would establish a universal time scale. Notions about time synchronization over distance come into play.

The Michelson-Morley Experiment of 1887.

The teaching of special relativity theory usually begins with mention of the Michelson-Morley experiment^[5] of 1887, so consideration of the relevance of that interferometry experiment to the theory is here appropriate. Einstein was inconsistent in his statements about the influence of the Michelson-Morley experiment on his creation of special relativity theory, at times claiming to have had no familiarity with it other than his awareness of allusions to it by others, at other times acknowledging it as the inspiration and experimental basis of his theory.

Basic Interferometry.

We detect light when it enters our eyes or a physical light detecting device, but we cannot see light otherwise as it travels. We imagine unseen light as a wave moving out from its source, and we model it as a single uniform frequency, for simplicity.

When two light waves merge, in-phase parts reinforce, while opposite-phase parts cancel. If two light beams originate from a single source, therefore in phase at the source, path length to the point of merging determines the phase of each beam, so at some points on a screen illuminated by the merging beams there is reinforcement and at other points, cancellation; points where there is reinforcement appear illuminated, while points where there is cancellation appear dark.

If a beam of light is projected towards a mirror whence it is reflected back toward the source, there will be alternating zones of dark (nodes) and light (anti-nodes) along the path; half the count of anti-nodes equals distance in wavelengths.

The standard interferometric method for length calibration employs light of a laser. Before the invention of lasers in 1960, experiments with light depended on incandescent sources that were polychromatic and less coherent.

The Michelson Interferometer.

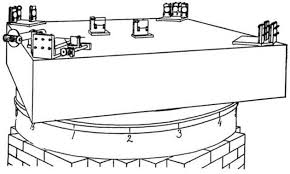
Michelson used the incandescent white light of an oil burning argand lamp. He constructed an interferometer with a half-silvered mirror to split the light into two beams for the two perpendicular arms of the interferometer. Each arm was equipped with mirrors at each end so the light would be reflected back and forth several times, the same in each arm, before merging to be seen by the observer sitting beside the apparatus. The total light-path length was constructed to be the same for the two arms. The physical apparatus was fastened to a stone slab to insure invariance of lengths. The stone slab was floated in mercury to permit smooth frictionless rotation in a horizontal plane. There was no clock or frequency standard involved, nor was there movement of the observer relative to the observed interference pattern. Michelson found, to his surprise, that rotating the interferometer caused no appreciable shift of the interference pattern.

Einstein's Special Theory of Relativity.

I shall not take time to describe all the features and implications of Einstein's special theory^[10] but only the foundations wherein a flaw resides. Empirical differences between classical relativity and special relativity are difficult to observe, supposedly being apparent for relative velocities that are a significant fraction of the speed of light.

The luminiferous ether, in debate about the Michelson-Morley experiment, was associated with the notion of a preferred or absolute frame of reference. Einstein, rather than trying to ascribe properties to the ether to account for the failure to detect motion relative it, decided to explore the conjecture that there was no ether. He persuaded himself that in absolutely featureless space absolute velocity and absolute rest were absurd notions. Consequently, he postulated that the speed of light must be the same relative to every frame of reference in which the laws of inertia were satisfied. In contrast, the argument to be presented here is that light-speed isotropy in empty space is a feature unique to a preferred frame of reference.

In presenting his special relativity, Einstein imagined timing a light signal from one clock to another clock. This would require a method of synchronizing the two clocks. The commonsense notion of simultaneous events is that the time of one event equals the time of the other. Oddly, Einstein assumed equivalence was satisfied by defining simultaneous by a protocol that ascribes half the time of a round trip to each direction. That is equivalent to claiming as true the dubious proposition that light speed is isotropic relative to any frame of reference.

We assume that this definition of synchronism is free from contradictions, and possible for any number of points; and that the following relations are universally valid:—

1. If the clock at B synchronizes with the clock at A, the clock at A synchronizes with the clock at B.
2. If the clock at A synchronizes with the clock at B and also with the clock at C, the clocks at B and C also synchronize with each other.

He did not retract his definition when, a few paragraphs later, he demonstrated the above assumptions were false.

... at the two ends A and B of the [moving] rod, clocks are placed which synchronize with the clocks of the stationary system.... with each clock there is a moving observer, and that these observers apply to both clocks the criterion established in § 1 for the synchronization of two clocks.... [and] thus find that the two clocks were not synchronous....

Rather than judging his definition of simultaneous to be flawed when he found it required different time scales for different frames of reference, he took that to mean that each observer would find the length and time determinations by a relatively moving observer to be longer than his own. He asserted that would be true for both; each would perceive the other's clocks to run slow and the other's measuring sticks to have contracted.

Einstein, also, derived the contraction factors, 1−(v/c)² parallel, and (1−(v/c)²)^½ perpendicular, in his special relativity paper before invoking “substituting for x′ its value,” as an abracadabra for the metamorphosis into Lorentz transformations which differed from the above by a factor of (1−(v/c)²)^½. Remarkably, even equations not containing x′ were metamorphosed in the process.

One-way Speed of Light.

Assumptions.

Taking care throughout that we do not assume our conclusion, we shall provisionally adopt the conjecture of FitzGerald. A Euclidean rest frame in which one-way light speed is isotropic is postulated. Material objects and proper spatial coordinates of moving inertial frames are contracted relative to rest frame coordinates.

The fraction of light speed of an inertial frame's velocity relative to the conjectured absolute rest frame is designated beta, β. Using time and length measure of the rest frame, the contraction expected in FitzGerald's theory would be by a factor (1 − β²) parallel to the motion and by (1 − β²)^½ perpendicular to the motion. For convenience, we define gamma, γ = 1/(1 − β²)^½. These FitzGerald factors are derived below^[↓], and, as mentioned above, were also derived by Michelson and by Einstein. If solid bodies do contract, spaces between unconnected solid bodies would appear greater relative to the moving frame than they do relative to the rest frame.

Velocity based time dilation could only be due to absolute velocity, not relative velocity, because relative velocity is not intrinsic to the frame in question. In any case, the slowing of atomic clocks and inversely proportionate lengthening of wavelength and of the moving object would, at any given point, affect all directions equally. The ratio of perpendicular to parallel contraction factors would remain γ = 1/(1 − β²)^½, so time dilation has no effect on the proposed experiment, and the experiment reveals nothing about time dilation. Moreover, factors claimed to affect time dilation are to be held to negligible variation.

Experimental Setup.

Consider an experimental local frame with a non-zero velocity β⋅c with respect to the conjectured rest frame. The experimental frame's absolute velocity is to be determined. Suppose we fix two atomic clocks sufficiently far apart for significant timing of light travel and eliminate refraction by evacuating the direct light path between the clocks. Let a light signal be sent forward from clock one to clock two where it is reflected back to clock one, with times of these events noted according to the respective clocks. Several trials are executed with differing orientation of the line between the clocks. In the example below the change of path orientation is effected by Earth rotation. The clocks need not be synchronized, but are assumed to measure time at the same rate throughout all trials; if not, rate differences must be known and compensated for. Clock one shall be regarded as the standard, so any synchronization error will be considered a clock-two error.

We shall be interested in:
Unknowns to be found:

• beta, β = v/c, the unknown vector quantity to be found, velocity of the experimental frame ÷ speed of light,
• β, magnitude of β
• α_β, right ascension of β
• δ_β, declination of β
• phi, φ, also unknown, the angle between the velocity, β, of the experimental frame and the directed line determined by the two clocks.
• t_err, clock-two synchronization error, (clock-one time = clock-two time − t_err)

• α_k, the right ascension in radians of clock two relative to clock one.
• δ_k, the declination in radians of clock two relative to clock one.
• t_A, the time on clock one when the light signal is emitted.
• t_B, the time on clock two when the light signal is reflected.
• t_C, the time on clock one when the returning light signal arrives.

• t_fwd = t_B − t_A, the nominal time taken by light to travel from clock one to clock two, (possibly inflated by t_err.)
• t_bck = t_C − t_B, the nominal time taken by light to travel from being reflected at clock two back to clock one, (possibly deflated by t_err.)
• t_dif = t_fwd − t_bck = 2t_B − t_A − t_C , (possibly inflated by a double synchronization error, 2t_err.)
• t_sum = t_fwd + t_bck = t_C − t_A, (time for round trip, no synchronization error.)
• t_ratio = t_dif / t_sum = ( 2t_B − t_A − t_C ) / ( t_C − t_A ), (a ratio strictly between one and minus one if, relative to some frame of reference, the clocks are synchronized; possibly inflated by 2t_err / σ)

[Note: Boldface is used for the vector value, if not boldfaced, the scalar magnitude is meant.]

The measure of the angle φ is frame of reference dependant. Accordingly, subscript zero φ₀ will denote rest frame value, and subscript beta φ_β will denote experimental frame value. These will be equal at angles, 0, ½⋅π, and π, (radian measure.)

Derivations.^[↑]

Figure 1 idealizes a trial of the experiment in rest frame scale. The two clocks, synchronized in the rest frame, move to the right at speed β⋅c, the points A, B, and C are the fixed rest frame locations where three events occur: at A, clock one emits a light signal at time t_A as it passes through point A; at B, clock two reflects the light signal at t_B; at C, the light signal and clock one arrive together at t_C. The point D is the location of clock one at t_B. So we have time intervals t_fwd = t_B − t_A and t_bck = t_C − t_B. The angle between the directed line DB determined by the two clocks and the velocity v = β⋅c of the experimental frame is labeled φ₀.

If the clocks are synchronized with respect to the rest frame, then for φ₀ = ½⋅π the ratio t_ratio = t_dif ÷ t_sum must be zero, because t_dif must be zero. However, for light path orientations at other angles φ₀ from β non-zero ratios t_ratio are expected, and parallel to β the maximum t_ratio is expected. In contrast to special relativity theory, wherein any inertial frame may be deemed at rest so t_ratio = 0 always.

Time dilation influences act as a scaling factor independent of direction and would have no effect on the ratio t_ratio or the angle φ.

Let us now derive equations for our variables of interest and the generalized transformations for any value of φ. Then, we will see the very factors derived by Michelson and Morley for φ = 0 and φ = ½⋅π.

The cosine law and quadratic formula yield solutions for t_fwd and t_bck in the triangles ADB and CDB respectively. First, t_fwd from triangle ADB in equations (1.1) through (1.3): 

( c tfwd )2 = ( β c tfwd )2 + d2 + 2 β c tfwd d cos(φ)	(1.1) cosine law for ΔADB
( β2 − 1 ) c2 tfwd2 + 2 β c d cos(φ) tfwd + d2 = 0	(1.2) eq 1.1 in standard quadratic form
tfwd = d0 ( β cos(φ0) + ( 1 - β2 sin2(φ0) )½ / ( c ( 1 - β2 ) )	(1.3) quadratic formula solution

Then, t_bck from triangle CDB in equations (1.4) through (1.6): 

	(1.4) cosine law for ΔCDB
	(1.5) eq 1.4 in standard quadratic form
	(1.6) quadratic formula solution

Now we see the time-difference, the time-sum, and the ratio t_ratio.

	(1.7) tdif
	(1.8) tsum
	(1.9) tratio

The experimental frame observer judges length by round-trip time of light, so d_β = ½c(t_fwd + t_bck). The equations for transformation of lengths between moving and ether frames are:

	(1.10) length transformation,      [recall: γ = 1/(1 − β2)½.]
	(1.11) parallel, sin 0 = 0
	(1.12) perpendicular,        sin ½π = 1

The spatial distance appears greater in the moving frame because the local measuring sticks are contracted.

Applying length transformations to the cosine function, cos φ_β = cos φ₀(1 – β² sin²φ₀)^–½, it turns out that t_ratio is a quite simple function of φ_β independent of clock rate:

(1.13) tratio(β,φβ)

The influence of unknown time dilation, i.e. clock rate change, must be isotropic, so it would enter these equations as a factor tau, τ; for example, d_β = τ γ²d₀ (1 − β² sin²φ₀)^½.

Expectations and Analysis.

For the Population of all Possible Orientations.

Polar coordinate plots with radial coordinate t_ratio as a function of angular coordinate φ_β for constant t_sum and β appear in figure 2.

For clocks absolutely synchronized, the plot of t_ratio for all values of φ is a circle that intersects the origin at φ = ½⋅π, and the diameter from the origin will equal β. The plot for φ ∈ [−½⋅π, ½⋅π] coincides with the plot for φ ∈ ([−π, −½⋅π]∪[½⋅π, π]).

tratio = β cos φβ

(1.13) (synchronized)

A synchronization error would make the plot a limaçon. It would be a looped limaçon if δ_β <  δ_k, except the plot could degenerate to a single loop if t_err is too great.

tratio = ( 2 terr / tsum ) + β cos φβ

(1.14) (not synchronized)

The 3-D celestial-coordinate plot of t_ratio is a limaçon rotated about the symmetry axis. If there are two loops, the celestial coordinates of the midpoint between the two extremal values of t_ratio will equal β, and the error ( 2 t_err / t_sum ) will be the maximal radial coordinate minus β.

Shown below in figures 3 and 4 are surface plots of t_ratio in the celestial coordinate system. The surfaces have symmetry axes through the origin parallel to β. In the absence of synchronization error, β is the point (t_ratio, α, δ) of the sphere farthest from the origin, possibly deduced from a minimum of four independent data points. A constant synchronization error would add a fixed 2t_err/σ to each data point, presenting an expanded spheroidal surface for t_ratio = β⋅cos φ_β + ( 2 t_err / t_sum ) of one sign and a contracted surface for t_ratio of the other sign. The two unknowns, β and synchronization error, ( 2 t_err / t_sum ), can both be determined from the full surface plot. The point midway between the surface's two absolutely maximal points is β. The value of t_ratio for φ = ½⋅π will be ( 2 t_err / t_sum ), which is also half the distance between the maximal points.

	figure 3 β = (0.001, αβ, 32.7°)
	figure 4 β = (0.001, αβ, −24.6°)

For a Sample Including All Observations of a Single Declination.

Figures 3 and 4 show a dark trace for sample with declination δ_k = 45° and t_ratio error = 0.0003 on a surface representing all possible orientations; in figure 3 β = (0.001, α_β, 32.7°), and in figure 4 with β = (0.001, α_β, −24.6°).

As Earth turns, an earth-bound horizontal light path of fixed length not parallel to the earth's rotational axis will present a cone of orientations of equal declination δ_k that includes (1) a path of maximal t_ratio at φ_min, (2) a path of minimal t_ratio at φ_max, and (3) equal φ pairs with equal t_ratio. Complete data for all α_k with δ_k and t_sum constant will reveal a symmetry plane containing β and therefore also α_β. It will remain to solve for t_err, δ_β, the sense of α_β and the magnitude β. This is a pattern of bilateral symmetry about a plane parallel to both β and the earth axis. A lack of synchronization does not alter the orientation of the symmetry plane provided the synchronization error is constant.

A Data Simulator / Solver is Available.

The solver calls for the user to supply observational data to a 2-D JavaScript array. Each data point is represented by an element of the array having five sub-elements consisting of the five observed quantities: α_k, δ_k, t_A, t_B, t_C. In a future improved version, the user will optionally specify change of velocity relative to the initial data point or specify the initial GPS time and exact terrestrial clock-one location so the solver can compute velocity changes from Earth's known motions.

From the five, (eventually eight,) observed quantities, the solver computes the elapsed times, t_sum, t_dif, and other required values including rectangular coordinates, x, y, and z corresponding to ( t_ratio, α_k, δ_k ).

The method of solution adapts the equation for a sphere, ( x - x_c )² + ( y - y_c )² + ( z - z_c )² = R² to the limaçon by subtracting the synchronization error part from the x, y, and z data, thus:

( x ( 1 - 2 t_err / t_dif ) - x_c )² + ( y ( 1 - 2 t_err / t_dif ) - y_c )² + ( z ( 1 - 2 t_err / t_dif ) - z_c )² - x_c² - y_c² - z_c² = 0 .

The equation is then expanded into linear terms for the unknowns:

( 4 t_dif / t_sum² ) t_err - ( 4 / t_sum²) t_err² + ( 2 x ) x_c + ( 2 y ) y_c + ( 2 z ) z_c + ( 4 x / t_dif ) t_err x_c + ( 4 y / t_dif ) t_err y_c + ( 4 z / t_dif ) t_err z_c = (t_dif / t_sum)²

The solution is obtained from a matrix equation using eight data points to provide an 8 × 8 matrix.

The simulator calls for the user to specify parameters for creation and graphical display of simulated data at equal intervals of right ascension and constant declination. The data output by the simulator is in the form required for input to the solver.

Clicking this link will run the simulator in a new browser tab.

Possibilities for a Terrestrial Test.

Possible sites for a long level course for carrying out such an earth-bound test might include a salt flat or a frozen lake. Sacrificing the ideal of an evacuated light path, a sheltered valley might serve. Specifically, a test site situated at the Bonneville Salt Flats (Lat. 40.736556, Long. -113.411537) with path up to ninety kilometer long and forward direction about 19° east of true north would give a constant 45° declination, but temperature fluctuations might be a problem. Under the ice of a Green Bay at the border between Wisconsin and Michigan, (Lat. 45.1, Long. -87.6) with path up to seventy kilometer long directed 26.5° east of true north to give a constant 19° declination, would be temperature stable and possibly sufficiently free of disturbing current. At certain seasons the air may be sufficiently clear and stable across La Garita Caldera in Colorado or Crater Lake in Oregon to run the test in air.

How accurate must clocks be to make a decisive test? Let us suppose a 90 km test course situated at the Bonneville Salt Flats. The relative velocity of the endpoints of the path would be less than 5 meter per second. The value of σ is 0.6 millisecond. Further, suppose β = (β, α_β, δ_β) = (0.001, 10°, −34°). The expected 0.00117 range of t_ratio, from 0.001⋅cos(169°) = -0.00098 to 0.001⋅cos(79°) = 0.00019, implies a one-way timing range of 0.35μs. Nanosecond timing accuracy would resolve this range into 350 parts, enough for a decisive test.

For highest precision, an extraterrestrial site, possibly the GPS system, would surely be best but would require more complex control and analysis.